Outils pour utilisateurs
Table des matières
Nombre dérivé et fonction dérivée
Notes et transcriptions du cours en ligne proposé par l'école Polytechnique (Université Paris-Saclay) sur la plateforme fun-MOOC et intitulé Polytechnique Collection Mathématiques: 1- Dérivation et Étude de fonctions.
Définitions
Taux d'accroissement
Soit une fonction définie sur un intervalle ouvert I à valeurs réelles.
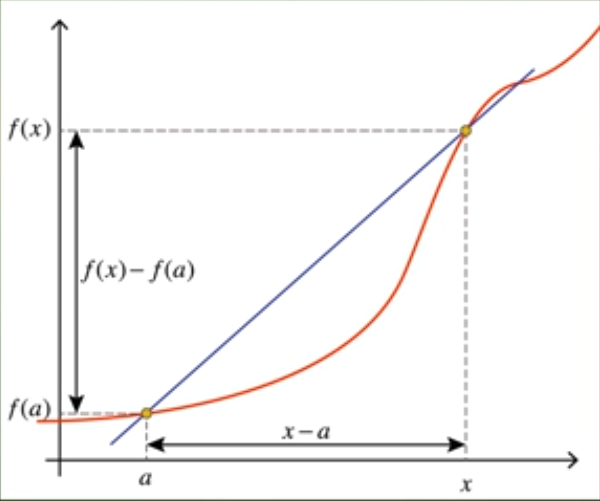
On appelle taux d'accroissement de la fonction entre deux éléments distincts
le nombre réel
représente la variation des images, ou variation sur l'axe vertical
;
représente la variation des antécédents, ou variation sur l'axe horizontal
.
On peut également le noter
Le taux d'accroissement c'est le quotient de la variation sur l'axe vertical par la variation sur l'axe horizontal. C'est aussi la pente ou le coefficient directeur de la droite passant par les deux points de coordonnées et
Nombre dérivé
On dit que la fonction est “dérivable en a” si son taux d'accroissement entre a et x admet une limite finie quand x tend vers a.
La limite est appelée le nombre dérivé de la fonction f en a et on le note
Autrement dit:
Une interprétation géométrique du nombre dérivé est abordée dans la séquence 4.
Si la fonction est dérivable en tout point de l'intervalle I, on dit que la fonction
est dérivable sur I et on désigne par
la fonction qui à tout point a de l'intervalle I associe le nombre dérivé de
en a.
La fonction est appelée la dérivée de la fonction
sur l'intervalle I.
En posant:
, on obtient une autre expression du nombre dérivé:
Exemples
Prenons des exemples de calculs de nombres dérivés.
Exemple 1
Commençons par un cas simple, déterminons le nombre dérivé en 1 de la fonction définie sur
par
Le taux d'accroissement entre 1 et x est
En factorisant le numérateur on obtient
En simplifiant par on on obtient
Lorsque x tend vers 1, on en déduit que tend vers 2 soit:
La fonction est donc dérivable en 1 et a pour nombre dérivé 2.
Exemple 2
Nous gardons la même fonction , mais nous allons chercher le nombre dérivé au point d’abscisse a, ce qui nous donnera la fonction dérivée de
.
On en déduit que quand x tend vers a:
La fonction est donc dérivable sur
et à pour dérivée la fonction
définie par
Exemple 3
Déterminons le nombre dérivé en 1 de la fonction définie par:
*
Pour simplifier l'expression, on cherche à factoriser le numérateur par
Le nombre dérivé en 1 de la fonction est égal à n.
Dérivée usuelles à connaître
- Si
alors
- Si
pour
* alors
- Si
alors
*+
- Si
alors
- Si
alors
- Si
alors
- Si
alors
*+
Généralisation
La formule de dérivation de la fonction est vraie pour tout n entier négatif (
).
La fonction correspondant au cas particulier ou
Par exemple pour on a
et
La formule est encore vraie pour c'est à dire
*