La transmission de l'information n’est pas toujours parfaite. En effet différents phénomènes peuvent altérer l’information reçue par le récepteur. Ceux-ci sont de deux types :

1. Des phénomènes internes aux systèmes communicants comme des erreurs logicielles ou matérielles peuvent provoquer la modification des informations binaires stockées et manipulées;
2. Des phénomènes externes comme des bruits électromagnétiques, l’endommagement du support physique ou des connecteurs, l’utilisation d’un support de mauvaise qualité provoquant un affaiblissement trop important peuvent empêcher un récepteur de décoder correctement le signal envoyé par l’émetteur.

Vous avez sans doute déjà expérimenté ces phénomènes en parlant à une autre personne dans un environnement bruyant ou lorsque celle-ci est trop éloignée.

Ces erreurs se mesurent généralement par le rapport entre:

• : le nombre de bits reçu erronés;
• : le nombre de bits transmis.

On désigne ce rapport BER, Bit Error Rate an anglais.

Le BER peut fortement varier d’un environnement à l’autre ou en fonction du type de support utilisé.

On mesure typiquement des BER de l’ordre de dans les réseaux sans fil c'est-à-dire un bit erroné par million de bits transmis. Dans les réseaux à supports tangibles il est courant de mesurer des BER de l’ordre de pour les supports métalliques et pour les supports optiques.

Même si les valeurs de BER actuelles semblent faibles, il convient au moins pour certains usages, de détecter les erreurs afin de savoir si l’information reçue est utilisable.

Ainsi avec un support physique sans fil fournissant un BER de et supportant un débit de 52Mb/s, 52 erreurs binaires sont en moyenne introduites par seconde. Si celui-ci est utilisé pour transporter des transactions bancaires les clients de la banque préféreront sans doute que les systèmes communicants soient capables de détecter celles-ci afin que leurs comptes ne soient pas débités de montants erronés.

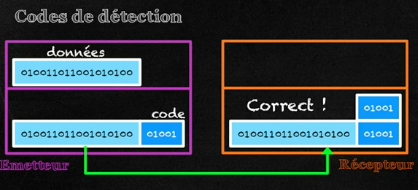
Afin de détecter les erreurs, une méthode consiste pour l’émetteur à ajouter une information redondante à l'information utile à transmettre. Ce code ajouté à l'information utile appelé code de contrôle est transmis en même temps.

Le code de contrôle va permettre au récepteur de détecter si les données ou le code lui même ont été modifiés lors de leur transfert. Pour cela le récepteur recalcule de la même manière le code de contrôle sur les données reçues:

• si le code qu’il a calculé sur les données reçues est le même que le code reçu il considère que les données sont correctes.
• Sinon il en conclut qu’une erreur s’est produite.

Un exemple simple de code de détection d’erreur est le bit de parité. Le bit de parité est une information codée sur un bit dont la valeur va dépendre du nombre de bits à 1 présents dans l' information utile transportée par l’émetteur :

• Si le nombre de bits à 1 dans l'information utile est en nombre impair, le bit de parité aura une valeur de 1;
• Si le nombre de bits à 1 dans l'information utile est en nombre pair, le bit de parité aura une valeur de 0.

Ce bit de parité permet de détecter un nombre impair d'erreurs sur l'information transmise entre l'émetteur et le récepteur.

Lorsque le récepteur reçoit les données, il compte le nombre de bits à ‘1’. Si le compte est impair il en déduit qu’au moins une erreur binaire s’est produite.

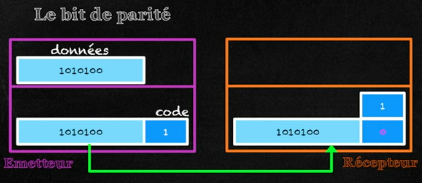
Prenons par exemple la suite binaire 1010100, celle-ci contient 3 bits à ‘1’, le bit de parité associé est donc ‘1’ de telle sorte que le total des bits à ‘1’ soit 4, un nombre pair. L’unité de donnée transmise sera alors 1010100 1.

Imaginons maintenant que pendant le transfert cette suite de bits soit altérée et que la valeur 1 du bit de parité soit transformée en 0.

La suite reçue vaudra alors 1010100 0, le bit de parité étant erroné. Le nombre bits à '1' reconnus par le récepteur sera alors de 3 ce qui lui permettra de détecter l'erreur de transmission.

On voit ici qu'avec cette technique, le récepteur est incapable de savoir ou l’erreur se trouve. Notons également qu’un nombre pair d’erreurs binaires ne peut être détecté puisque deux erreurs binaires vont se compenser.

Il existe des codes de détection plus complexes tels que les codes de redondance cyclique ou CRC qui permettent de détecter un plus grand nombre d’erreurs en contrepartie d’une taille plus importante (typiquement 16 ou 32 bits) et d’une méthode de calcul plus complexe.

Il existe également des codes de correction d’erreur permettant comme leur nom l’indique de corriger les bits erronés. Pour une capacité de correction égale à une capacité de détection (par exemple la capacité de détecter 4 bits erronés et la capacité de les corriger) le code de correction utilisera typiquement un code de taille plus importante. On aura donc plutôt tendance à utiliser ces codes de lorsque le BER est élevé.

Il existe une grande variété de codes de détection et de correction d'erreurs, chacun ayant des caractéristiques propres. Ce sont les besoins des applications qui détermineront quels codes il est pertinent d'utiliser : le nombre d'erreurs qu'elles peuvent supporter sans être perturbées.

Nous allons donc utiliser un mécanisme de détection ou de correction de telle sorte à améliorer le BER brut fournit par la couche physique afin de satisfaire cette contrainte.

On choisit un code par rapport à un autre afin que la probabilité de ne pas détecter une erreur pour un environnement donné soit acceptable pour une application donnée et que son coût le soit également.

Petit exemple pour terminer cette séance. Avec le bit de parité, l’émetteur envoie la suite binaire 11010 1, le récepteur reçoit la suite 11010 0. Que peut faire le récepteur ?

1. Le récepteur voit que la suite reçue est bonne et peut l’utiliser.
2. Le récepteur voit que la suite reçue est erronée mais il peut l’utiliser car l’erreur porte sur le bit de parité.
3. Le récepteur voit que la suite reçue est erronée et il ne peut pas l’utiliser.

La réponse correcte est la n°3. Lorsqu’il reçoit 11010 0, le récepteur détecte une erreur puisque le nombre de bit à ‘1’ est impair. Cependant cette erreur pourrait venir de la transformation du 2eme bit de ‘0’ à ‘1’ ou de la transformation du 5eme de ‘1’ en ‘0’. Il ne peut pas savoir quelles données sont altérées : il ne peut donc pas les utiliser.

◁ Précédent | ⌂ Sommaire | Suivant ▷